成為大叔後又繼續的數理之路：半路出家的微積分入門

有點碎念的前言

自從高中畢業後，我就沒有再碰數學了，之後的職涯也跟數理八竿子打不著。

想不到在各種因緣際會之下開始接觸程式，我又再重度回數學的懷抱。

還是學生的時候，我的數學成績並沒有特別突出，甚至可以說是墊底的那種。

即便如此，我並不討厭數學，甚至還著迷於它的深奧難解。

這種Ｍ傾向，真的可以說是：「數學虐我千百遍，我待數學如初戀。」

也可能是補償心理在作祟吧？當初因為家裡的因素而沒有去讀大學（這年頭，或跟我同世代的人，沒有大學畢業反而很罕見吧？），這讓我更好奇大學到底在學些什麼東西。

因此，除了寫程式會需要研究演算法外，最近出於一些需要，我又開始接觸微積分的一些概念。

可能會有人覺得我有毛病，都已經是大叔了，也沒有學生的身份，如果不是靠那個吃飯，誰會想研究那麼複雜又令人昏昏欲睡的東西呢？

說實在話，在沒有外力逼迫的前提下，這樣自主研究數學其實還挺有意思的。

有心理學研究指出外在驅力可能影響甚至破壞一個人的內在動機，。

如果一個人對某件事感興趣，你用利誘（金錢或某些外在好處），或是脅迫的方式，都會降低一個人對這件事的興趣。

感興趣的事都可能因為騷操作 debuff 了，更何況原本沒有特別感興趣的事。

我們的教育體制看起來偏坦 STEM（理工科），但它其實更擅長把「培養」這回事搞砸。

體制教育與其說是培養，其實比較接近篩選，撐不過前面的關卡就直接淘汰，發展潛能，多樣性什麼的只不過是用來隱藏這部無情篩選機器的口號罷了。

而且那些篩選關卡究竟有沒有必要？長期來說利有沒有大於弊？我看掌握這套機器的主事者應該也沒能給出一個好的答案。

扯遠了，我想說的是，其實數學真的很有意思，即便你不再需要考試，應該說不需要為了應付考試更好，你更能在不被外力干擾下，體會數學的奧妙之處。

伽利略對數學是這麼推崇：「數學是神用來書寫宇宙的語言。」(“Mathematics is the language with which God has written the universe.”)

除了神創造的世界外，我們現今的科技（包括你口袋裡的 iPhone）全都是建立數學之下，你說這麼神奇又這麼與我們息息相關的東西，怎麼會不讓人想一探究竟？

很多人覺得數學抽象又艱深，在學生時代的考試被爆打後，就開始視數學為畏途，但我認為人人都能學會數學。

料理鼠王這部皮克斯經典動畫中，有個角色叫食神，他說過一句話讓我印象很深刻：「料理非難事」（Anyone can cook.）。

我也認為「數學非難事」（Anyone can learn math.），只要能懂邏輯（我相信大部分的人都能搞懂），人人都可以學會數學。

（筆者註：數學非難事（Anyone can learn math.），跟「成為最頂尖的數理學者，拿下諾貝爾獎、菲爾茲獎（數學界的最高榮譽）」，這是兩回事。這就跟「料理非難事」與「成為世界頂尖大廚」也是兩回事。我相信你的邏輯一定能區分出兩者的不同）

你不一定要當頂尖的數學高手，但你還是可以學習數學、體會它的奧妙。

半路出家的微積分入門

高等數學的概念有兩大雙璧：微積分與線性代數。

尤其是微積分，許多人將它視為艱深複雜的代名詞，避之唯恐不及，就像《One Piece》（航海王）故事中的霸氣一樣，很多人可能看到「微積分」這三個字就被震攝住了，只差沒口吐白沫昏倒。（不過會令人昏昏欲睡倒是真的）

所以這一次筆者想來談談惡名昭彰的微積分。它是很多接觸過數學的人的惡夢，由於我沒有在教育體制內修過微積分的經驗，所以無法體會這門學分被當掉是什麼感覺，但我還是想跟你分享，我接觸微積分的經驗。

許多偉大的科學家都認為，想知道一個人到底懂不懂某個複雜的概念，那就看他有沒有辦法，用簡單明瞭的方式來描述這個概念。

反過來說，如果我們可以將一個很複雜的概念，先從某個能夠簡單理解的角度切入，這會不會是一個好的入門方式呢？這樣一來，你才不會一下子被太多難點搞到頭昏，然後勸退。

這就像玩 RPG 遊戲，你不會在剛出新手村就直接去挑戰最終 Boss。

而是先練功，靠著階段性的關卡來累積實力，最後才叩關最終 Boss。（這裡不討論 Speed Run 或是一些神人級的特殊玩法，那是特例）

我認為大多數人的數學之路之所以被勸退，都是因為才剛出新手村就急著去打王，被慘電後就認定自己不行，以上狀況的解方就是乖乖地從新手村開始，確實提升等級後再前進。

所以，什麼是微分？

微積分學（Calculus）這個主題，可以拆分成「微分」（differential）與「積分」（integral）兩大概念。

我們先從微分談起。

前面有提到，我們盡可能以簡單明瞭的方式切入一個概念。

只要掌握好它，之後都能以此為起點，穩扎穩打地逐步擴展。

這也是筆者個人相當喜歡的一個原則：如果沒必要，就先別把事情搞得複雜，也就是奧坎剃刀法則的核心精神。

所以這個簡單的概念就是：所謂的微分，就是去找出某個函數的切線斜率。

在微積分的概念出現之前，人類看世界的眼光是相對靜態的，我們只能理解平均而言的變化狀況，例如平均速度。

在中學的時候，我們就學過，平均速度的意思是，在某一段時間內，某人或某物移動的距離（位移）。

也就是移動距離除以某段時間。

它的公式可以寫成像下面這樣的：

$$\bar{v} = \frac{\Delta x}{\Delta t}$$

畫成函數圖形來看會更清楚：

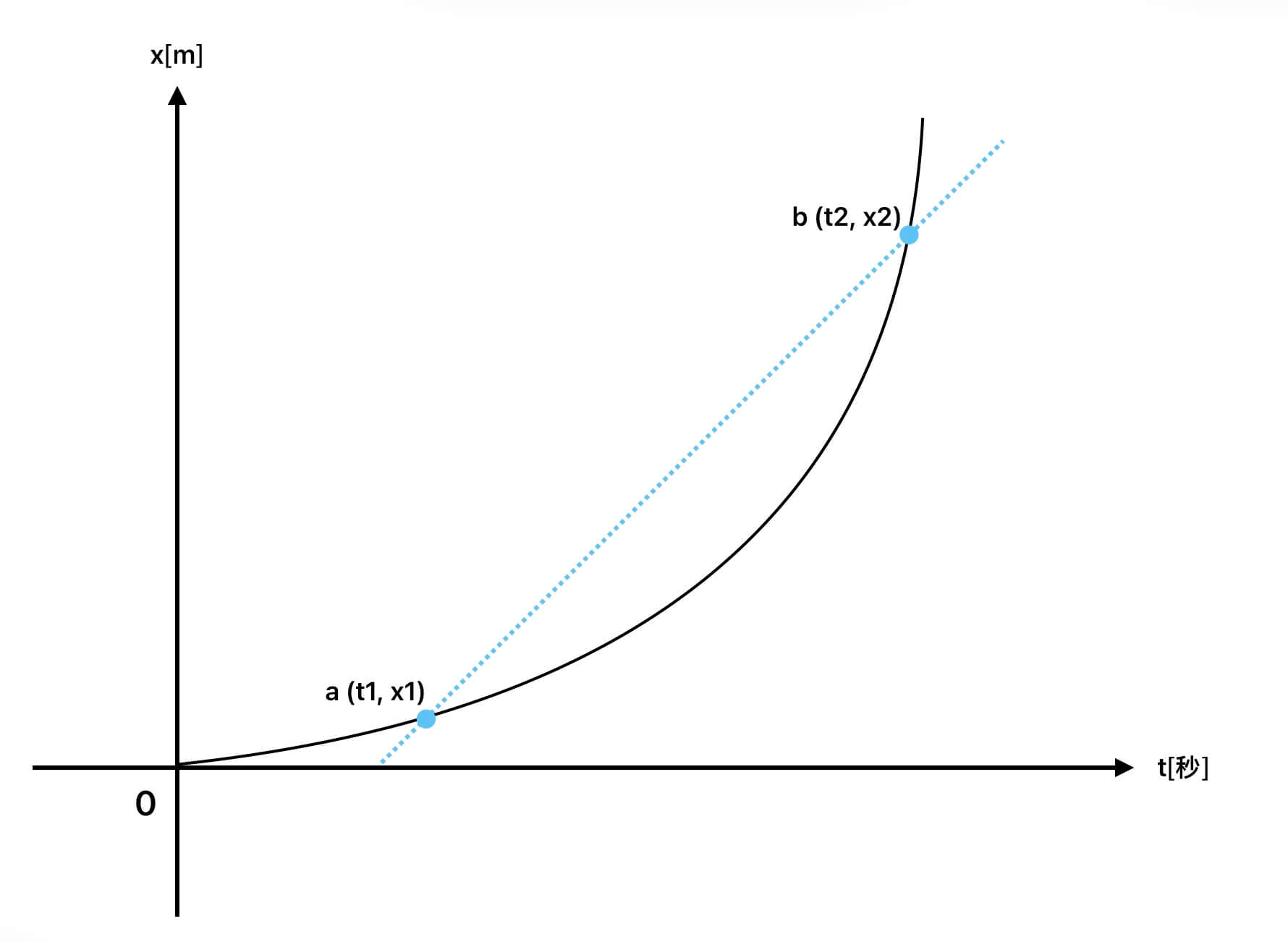
a 點到 b 點的平均速度可以用以下的方式表示：

$$\frac{x_2 - x_1}{t_2 - t_1} = \frac{\Delta x}{\Delta t}$$

從以上的圖形我們可以發現，平均速度就是 x-t 圖中，函數圖形兩點連線（藍色虛線）的斜率。

切線斜率

後來出現了一位天才，他想說：如果我把這一段時間的區間，取得很短很短會發生什麼事？

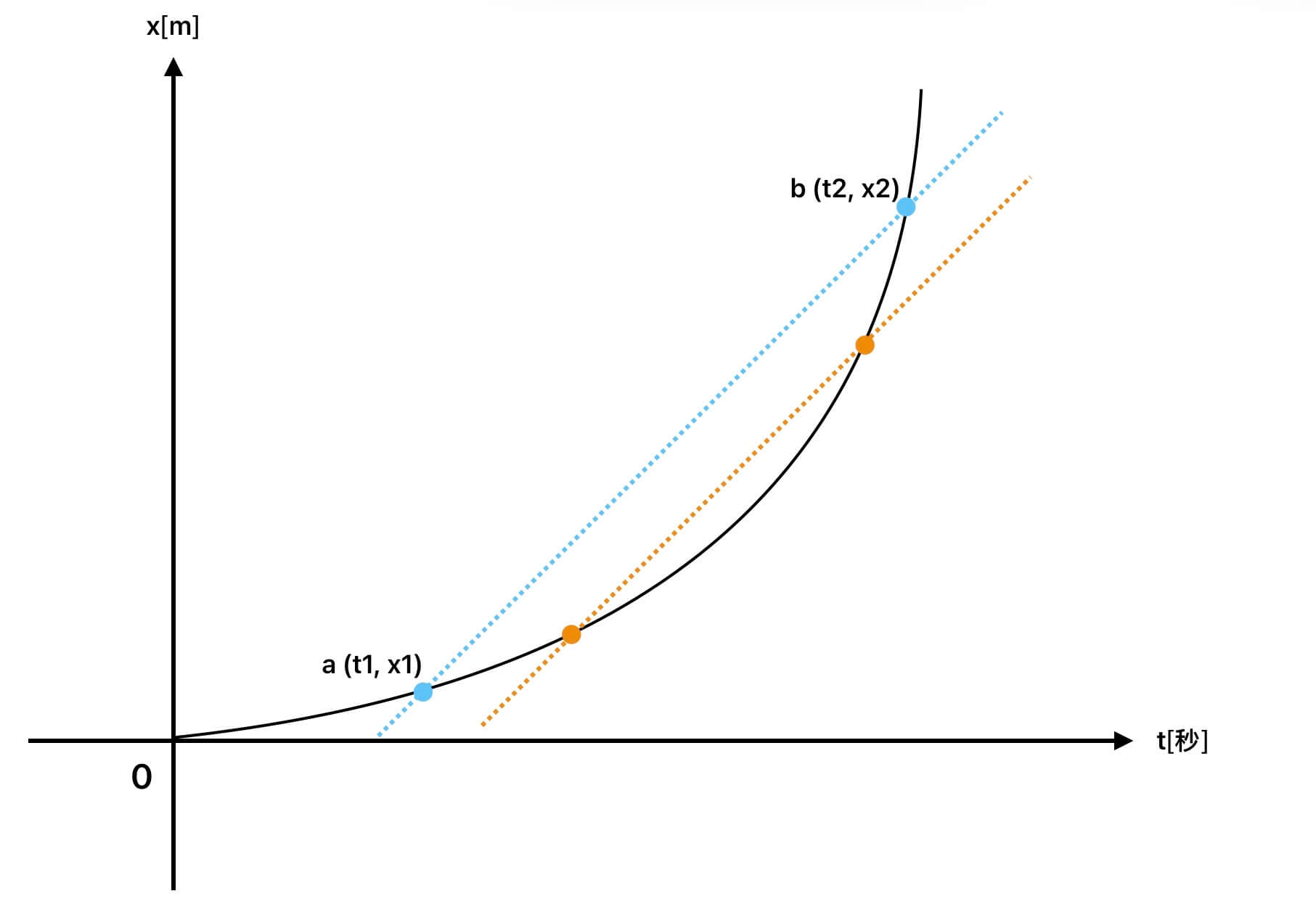
就像上面圖形中的橘色虛線。

既然我們在函數中，將時間區間取短，那麼函數上對應點的位移也會跟著改變，當這個區段越取越小後，就會發生一件事，你可以觀察一下，以下面圖形中的紅色虛線：

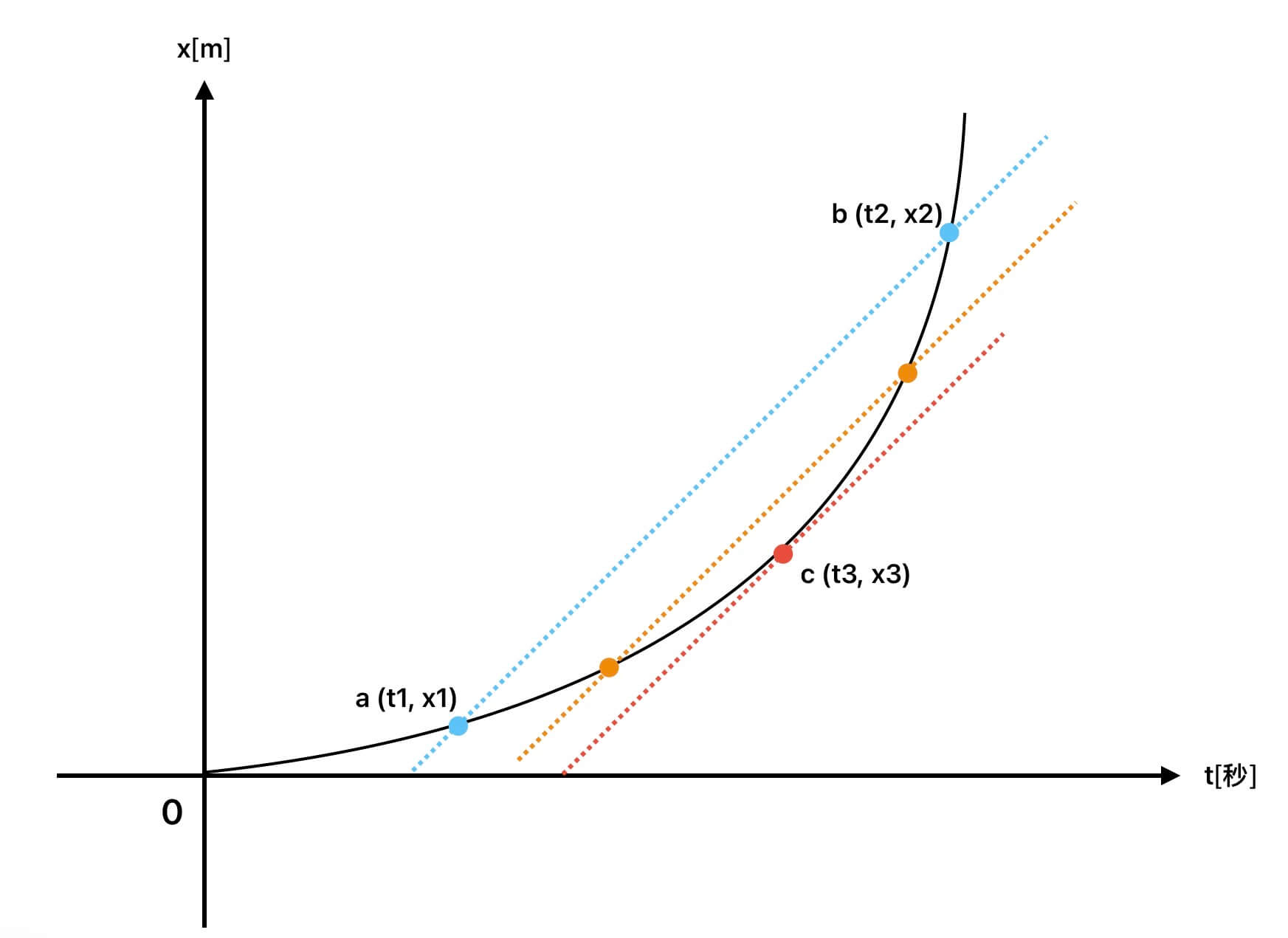
看到了嗎？兩點的斜率逐漸變成 c 點的切線斜率。

這一個點的切線斜率，就是所謂的瞬時速度。

當我們將平均速度的時間區間越取越小時，瞬時速度的概念就出現了，就是 x-t 線圖上的切線斜率。

所以瞬時速度的表示方式為：

$$v = \lim_{\Delta t \to 0} \frac{\Delta x}{\Delta t}$$

我們可以看到，極限（時間區間趨近於 0）的概念出現了。

找出函數上某一點的切線斜率的過程也稱作求導數。

所以，導數可以看成是一個函數在某個點上的切線斜率，也就是某段極小區間的變化率。

在數學上，一個函數曲線中的「每一個點」的切線斜率，也可以用另一個函數表示。

這個表示切線斜率的「新函數」，就是原本函數的微分。

我們通常會在原函數標上一撇來表示微分，就像這樣：

$$f'(x) = y' = \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x}$$

如果要找出函數某一點的導數（切線斜率），就會這樣子表示：

$$f'(a) = \lim_{h\to 0}{\frac {f(a+h)-f(a)}{h}}$$

其中，${a}$ 代表函數上的某個點，而 ${h}$ 沒有特別的含義，只是將 ${\Delta x}$ 換一個變數表示，代表某個趨近於 0 的數值。

小結

如果你可以理解上述推演過程，你其實就已經掌握住微分的初步概念了。

什麼？就這樣嗎？這就是微分？當初我在了解之後也嚇了一跳！

當然不只這樣啦！後面還有各種噁心人的進階概念變種。

但先別急著打王，我們不是說好要先從簡單明瞭的方式切入，練完功之後才前進不是嗎？

我在網路上曾看過對微積分的一種解釋是，微分你可以想成是強化版本的減法，所以之後要來談的積分就是加法的強化版本！

補充

微積分的起點，就是前面提到的天才，力學之父－牛頓，他為了更好地描述物體運動而發展出來的數學理論。

除了我們所知的牛頓力學外，這位天才也是微積分學的奠基者之一。

除了牛頓外，微積分學還有另一位奠基者，就是萊布尼茲（Gottfried Wilhelm Leibniz），他也是符號學的大師。

萊布尼茲將微分寫成以下形式：

$$f'(x) = y' = \frac{dy}{dx}$$

這種表示法，類似於一般的斜率表示方式：

$$\frac{\Delta y}{\Delta x}$$

原本的三角形符號（delta）變成 d ，這讓微分後續的一些進階計算變得相當直觀且容易處理。